Baik, mari kita buat artikel tentang contoh indikator soal matematika kelas 8 SMP semester 2, lengkap dengan penjelasannya.

Memahami Indikator Soal Matematika Kelas 8 Semester 2: Panduan Lengkap dengan Contoh dan Penerapannya

Pendahuluan

Dalam dunia pendidikan, evaluasi merupakan bagian integral dari proses pembelajaran. Evaluasi dilakukan untuk mengukur sejauh mana peserta didik telah memahami materi yang diajarkan. Salah satu instrumen penting dalam evaluasi adalah soal ujian atau tes. Namun, soal yang baik tidaklah dibuat secara acak. Pembuatan soal harus didasarkan pada indikator soal yang jelas dan terukur.

Artikel ini akan membahas secara mendalam tentang indikator soal matematika kelas 8 SMP semester 2. Kita akan mengulas pengertian indikator soal, fungsi dan manfaatnya, serta memberikan contoh-contoh indikator soal beserta penjelasannya. Tujuannya adalah untuk memberikan pemahaman yang komprehensif bagi guru, siswa, dan pihak-pihak terkait tentang bagaimana merumuskan dan memahami indikator soal matematika yang efektif.

Apa Itu Indikator Soal?

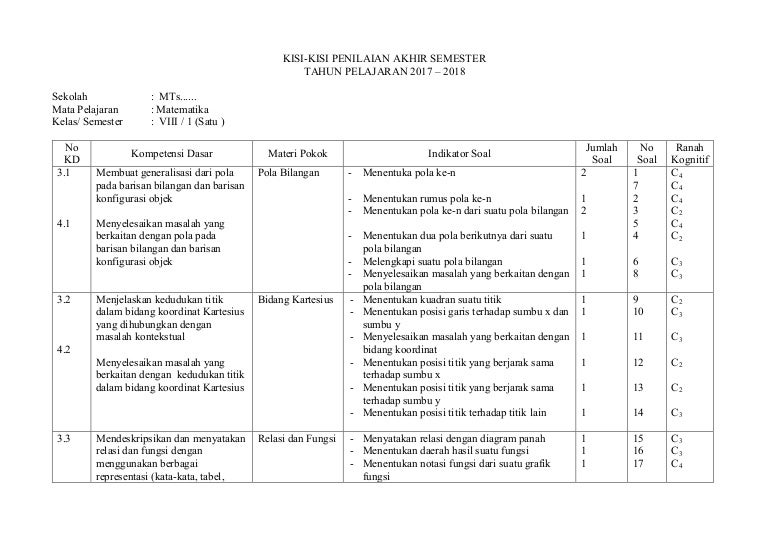
Indikator soal adalah rumusan kemampuan yang lebih spesifik yang harus dikuasai oleh peserta didik setelah mempelajari suatu kompetensi dasar (KD). Indikator soal merupakan penjabaran dari KD dan digunakan sebagai acuan dalam penyusunan soal. Dengan kata lain, indikator soal adalah "jembatan" antara KD dan soal yang akan diujikan.

Indikator soal yang baik harus memenuhi beberapa kriteria, yaitu:

• Sesuai dengan KD: Indikator soal harus relevan dan sejalan dengan KD yang ingin diukur.
• Spesifik: Indikator soal harus dirumuskan secara spesifik dan jelas, sehingga tidak menimbulkan penafsiran ganda.
• Terukur: Indikator soal harus dapat diukur melalui soal yang dibuat.
• Menggunakan Kata Kerja Operasional (KKO): Indikator soal sebaiknya menggunakan KKO yang terukur, seperti "menentukan", "menghitung", "menganalisis", "membandingkan", dan sebagainya.
• Memuat Materi: Indikator soal harus menyebutkan materi yang akan diujikan.
• Memuat Konteks (Jika Perlu): Indikator soal dapat memuat konteks tertentu agar soal lebih aplikatif dan relevan dengan kehidupan sehari-hari.

Fungsi dan Manfaat Indikator Soal

Indikator soal memiliki fungsi dan manfaat yang signifikan dalam proses evaluasi pembelajaran, antara lain:

• Sebagai Pedoman Penyusunan Soal: Indikator soal memberikan arah yang jelas bagi guru dalam menyusun soal. Guru dapat memastikan bahwa soal yang dibuat sesuai dengan KD yang ingin diukur dan memiliki tingkat kesulitan yang sesuai.
• Memastikan Validitas Soal: Dengan menggunakan indikator soal sebagai acuan, guru dapat memastikan bahwa soal yang dibuat valid, yaitu mengukur apa yang seharusnya diukur.
• Meningkatkan Kualitas Evaluasi: Indikator soal membantu meningkatkan kualitas evaluasi karena soal yang dibuat lebih terstruktur, terarah, dan relevan dengan materi yang diajarkan.
• Memberikan Informasi Diagnostik: Hasil evaluasi yang didasarkan pada indikator soal dapat memberikan informasi diagnostik tentang kekuatan dan kelemahan siswa dalam memahami materi. Informasi ini dapat digunakan untuk memberikan tindak lanjut yang tepat bagi siswa.
• Transparansi: Indikator soal dapat memberikan transparansi kepada siswa tentang apa yang diharapkan dari mereka dalam evaluasi. Siswa dapat menggunakan indikator soal sebagai panduan belajar.

Contoh Indikator Soal Matematika Kelas 8 SMP Semester 2

Berikut adalah beberapa contoh indikator soal matematika kelas 8 SMP semester 2, yang dikelompokkan berdasarkan materi pokok:

1. Teorema Pythagoras

• KD: Menerapkan teorema Pythagoras untuk menyelesaikan masalah.
• Indikator Soal:
  • Disajikan gambar segitiga siku-siku, siswa dapat menentukan panjang sisi yang belum diketahui menggunakan teorema Pythagoras.
  • Disajikan masalah kontekstual yang berkaitan dengan teorema Pythagoras (misalnya, menghitung tinggi tiang yang disandarkan pada tembok), siswa dapat menyelesaikan masalah tersebut.
  • Siswa dapat menentukan jenis segitiga (siku-siku, lancip, atau tumpul) berdasarkan panjang sisi-sisinya.
  • Siswa dapat menghitung diagonal ruang kubus atau balok.

Contoh Soal (Sesuai dengan Indikator):

1. Perhatikan gambar segitiga siku-siku berikut. Jika panjang AB = 6 cm dan BC = 8 cm, maka panjang AC adalah…
2. Sebuah tangga dengan panjang 5 meter disandarkan pada tembok. Jarak ujung bawah tangga dengan tembok adalah 3 meter. Tinggi tembok yang dapat dicapai tangga adalah…
3. Panjang sisi-sisi sebuah segitiga adalah 5 cm, 12 cm, dan 13 cm. Jenis segitiga tersebut adalah…
4. Sebuah kubus memiliki panjang rusuk 10 cm. Hitunglah panjang diagonal ruang kubus tersebut.

2. Lingkaran

• KD: Menjelaskan unsur-unsur lingkaran dan hubungannya.
• KD: Menghitung keliling dan luas lingkaran.
• Indikator Soal:
  • Siswa dapat menyebutkan unsur-unsur lingkaran (jari-jari, diameter, busur, tali busur, apotema, juring, tembereng).
  • Siswa dapat menghitung keliling lingkaran jika diketahui jari-jari atau diameter.
  • Siswa dapat menghitung luas lingkaran jika diketahui jari-jari atau diameter.
  • Siswa dapat menghitung panjang busur dan luas juring lingkaran dengan sudut pusat tertentu.
  • Disajikan masalah kontekstual yang berkaitan dengan lingkaran (misalnya, menghitung luas taman berbentuk lingkaran), siswa dapat menyelesaikan masalah tersebut.
  • Siswa dapat menghitung luas tembereng.

Contoh Soal (Sesuai dengan Indikator):

1. Sebutkan 3 unsur lingkaran!
2. Sebuah lingkaran memiliki jari-jari 7 cm. Hitunglah keliling lingkaran tersebut!
3. Sebuah lingkaran memiliki diameter 14 cm. Hitunglah luas lingkaran tersebut!
4. Sebuah lingkaran memiliki jari-jari 10 cm. Hitunglah panjang busur yang menghadap sudut pusat 60 derajat!
5. Sebuah taman berbentuk lingkaran memiliki diameter 20 meter. Hitunglah luas taman tersebut!
6. Tembereng dibentuk oleh tali busur yang panjangnya 10 cm dan jari-jari lingkaran 10 cm. Hitung luas tembereng tersebut.

3. Garis Singgung Lingkaran

• KD: Menjelaskan garis singgung persekutuan luar dan persekutuan dalam dua lingkaran dan cara melukisnya.
• Indikator Soal:
  • Siswa dapat membedakan antara garis singgung persekutuan luar dan garis singgung persekutuan dalam dua lingkaran.
  • Siswa dapat menghitung panjang garis singgung persekutuan luar dua lingkaran jika diketahui jari-jari kedua lingkaran dan jarak antara kedua pusat lingkaran.
  • Siswa dapat menghitung panjang garis singgung persekutuan dalam dua lingkaran jika diketahui jari-jari kedua lingkaran dan jarak antara kedua pusat lingkaran.
  • Disajikan masalah kontekstual yang berkaitan dengan garis singgung lingkaran (misalnya, menghitung panjang sabuk yang menghubungkan dua roda), siswa dapat menyelesaikan masalah tersebut.

Contoh Soal (Sesuai dengan Indikator):

1. Jelaskan perbedaan antara garis singgung persekutuan luar dan garis singgung persekutuan dalam dua lingkaran!
2. Dua lingkaran memiliki jari-jari 5 cm dan 3 cm. Jarak antara kedua pusat lingkaran adalah 10 cm. Hitunglah panjang garis singgung persekutuan luar kedua lingkaran tersebut!
3. Dua lingkaran memiliki jari-jari 7 cm dan 2 cm. Jarak antara kedua pusat lingkaran adalah 13 cm. Hitunglah panjang garis singgung persekutuan dalam kedua lingkaran tersebut!
4. Dua buah roda dengan jari-jari 20 cm dan 10 cm dihubungkan dengan sabuk. Jarak antara kedua pusat roda adalah 50 cm. Hitunglah panjang sabuk yang dibutuhkan!

4. Bangun Ruang Sisi Datar

• KD: Menentukan luas permukaan dan volume kubus, balok, prisma, dan limas.
• Indikator Soal:
  • Siswa dapat menghitung luas permukaan kubus, balok, prisma, dan limas.
  • Siswa dapat menghitung volume kubus, balok, prisma, dan limas.
  • Disajikan masalah kontekstual yang berkaitan dengan bangun ruang sisi datar (misalnya, menghitung volume kolam renang berbentuk balok), siswa dapat menyelesaikan masalah tersebut.
  • Siswa dapat menghitung luas permukaan bangun ruang gabungan.
  • Siswa dapat menghitung volume bangun ruang gabungan.

Contoh Soal (Sesuai dengan Indikator):

1. Sebuah kubus memiliki panjang rusuk 8 cm. Hitunglah luas permukaan kubus tersebut!
2. Sebuah balok memiliki panjang 10 cm, lebar 5 cm, dan tinggi 4 cm. Hitunglah volume balok tersebut!
3. Sebuah kolam renang berbentuk balok memiliki panjang 15 meter, lebar 8 meter, dan kedalaman 2 meter. Hitunglah volume air yang dapat ditampung kolam renang tersebut!
4. Sebuah bangun ruang terdiri dari kubus dengan sisi 5 cm yang ditumpuk di atas balok dengan panjang 10 cm, lebar 5 cm, dan tinggi 3 cm. Hitunglah luas permukaan bangun ruang tersebut.
5. Sebuah bangun ruang terdiri dari kubus dengan sisi 5 cm yang ditumpuk di atas balok dengan panjang 10 cm, lebar 5 cm, dan tinggi 3 cm. Hitunglah volume bangun ruang tersebut.

Penutup

Indikator soal merupakan elemen penting dalam penyusunan soal matematika yang berkualitas. Dengan memahami dan menerapkan prinsip-prinsip perumusan indikator soal yang baik, guru dapat menghasilkan soal yang valid, reliabel, dan relevan dengan kebutuhan peserta didik. Artikel ini diharapkan dapat memberikan panduan yang komprehensif bagi guru, siswa, dan pihak-pihak terkait dalam memahami dan memanfaatkan indikator soal matematika kelas 8 SMP semester 2. Dengan evaluasi yang baik, diharapkan proses pembelajaran dapat ditingkatkan dan tujuan pembelajaran dapat tercapai secara optimal.

Semoga artikel ini bermanfaat!